Simulating the Monty Hall Problem with a Monte Carlo method. The paradox is real!

The Monty Hall problem is a brain teaser, in the form of a probability puzzle (Gruber, Krauss and others), loosely based on the American television game show Let's Make a Deal and named after its original host, Monty Hall. The problem was originally posed (and solved) in a letter by Steve Selvin to the American Statistician in 1975 (Selvin 1975a), (Selvin 1975b). It became famous as a question from a reader's letter quoted in Marilyn vos Savant's "Ask Marilyn" column in Parade magazine in 1990 (vos Savant 1990a):

“

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?

Vos Savant's response was that the contestant should switch to the other door (vos Savant 1990a). Under the standard assumptions, contestants who switch have a 2/3 chance of winning the car, while contestants who stick to their initial choice have only a 1/3 chance.
(link: https://en.wikipedia.org/wiki/Monty_Hall_problem)

 Many scientist, including Paul Erdös, refused to accept the paradox, until they were convinced by a simulation.

In this post I want to show a project that I wanted to do for a long time: to test the Monty Hall Problem with a computer simulation to analyze the results. Surprisingly, when the number of simulations was big enough (around a 1000 simulations) the results tended to aproximate to the 1/3 probability when the player decided to stay and tended to 2/3 when the player decided to switched the door. The paradox is real.

What I did is basically a Monte Carlo method, which is a type of stochastic model, to prove the paradox.

You can find the code of the simulation I developed in C language in the following link. And you can download this executable file to test it yourself (30kb). It's not perfect, there's a lot of optimization to be done, but it works. And, surprisingly for me, the paradox is true. I was one of the guys who couldn't believe the paradox and thought there was some kind of gambler's biase. But I was wrong, the simulation doesn't lie. So if you're a non-believer like me, this simulation and the many others around the WWW, should be enough to convince you. Science is a lot of things, but at the end of the day, science is the acceptance of what it works and the rejection of what it doesn't.

Monte Carlo methods (or Monte Carlo experiments) are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. Their essential idea is using randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three distinct problem classes:^[1] optimization, numerical integration, and generating draws from a probability distribution.

The Monte Carlo method was invented by Stanislaw Ulam in 1940 while he was working in Project Manhattan, in Los Alamos, USA (the nuclear bomb project). Ulam was playing a famous card game, the Solitaire, when he wondered what was the best strategy to solve the game.

The best approach, would be to find a deductive probability solution, but he decided to test the game as many times as possible, count the inputs and outputs, and figure out with statistics the best inputs to obtain the best outputs. Of course, in order that the experiment is successful, you need a sample of simulations as big as you can, otherwise the results won't be accurate.

The Monte Carlo method is not a valid method in mathemathics to prove anything. As we know, maths are tricky, inductive solutions are not always true while deductive solutions tend to be much better since it respects the scientific method,  which is based in the hypothetical deductive reasoning principle, which has demonstrated to be the best solution in the modern era to solve problems.

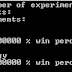
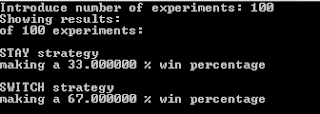
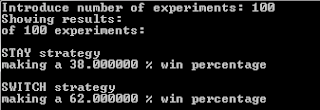
If you are too lazy to test the simulation by yourself, here I'll show you some of the results:

As you can see, the more number of simulations, the more accurate result. For a 100 million simulations, whe get a 33.33206% (good approximation of 1/3) and 66.666794% (good approximation of 2/3).